后缀自动机
$\ \ \ \ \ \ \ \,$关于后缀自动机性质的复习笔记:
$\ \ \ \ \ \ \ \,$后缀自动机是一个可以解决大多数字符串问题的字符串数据结构,可以识别该字符串的所有子串,其时空复杂度也比较优秀,对于一个字符集大小为$m$,长度为$n$的字符串,建立一个后缀自动机的时间复杂度为$O(nm)$,空间复杂度为 $O(2nm)$。
$\ \ \ \ \ \ \ \,$讲后缀自动机的博客很多,这里直接给出模板,重点讲讲后缀自动机长什么样子,怎么用它:
1 | struct Suffix_Automaton{ |
$\ \ \ \ \ \ \ \,$对于一个串 $abcabbca$,我们建立的后缀自动机就是这个样子的:
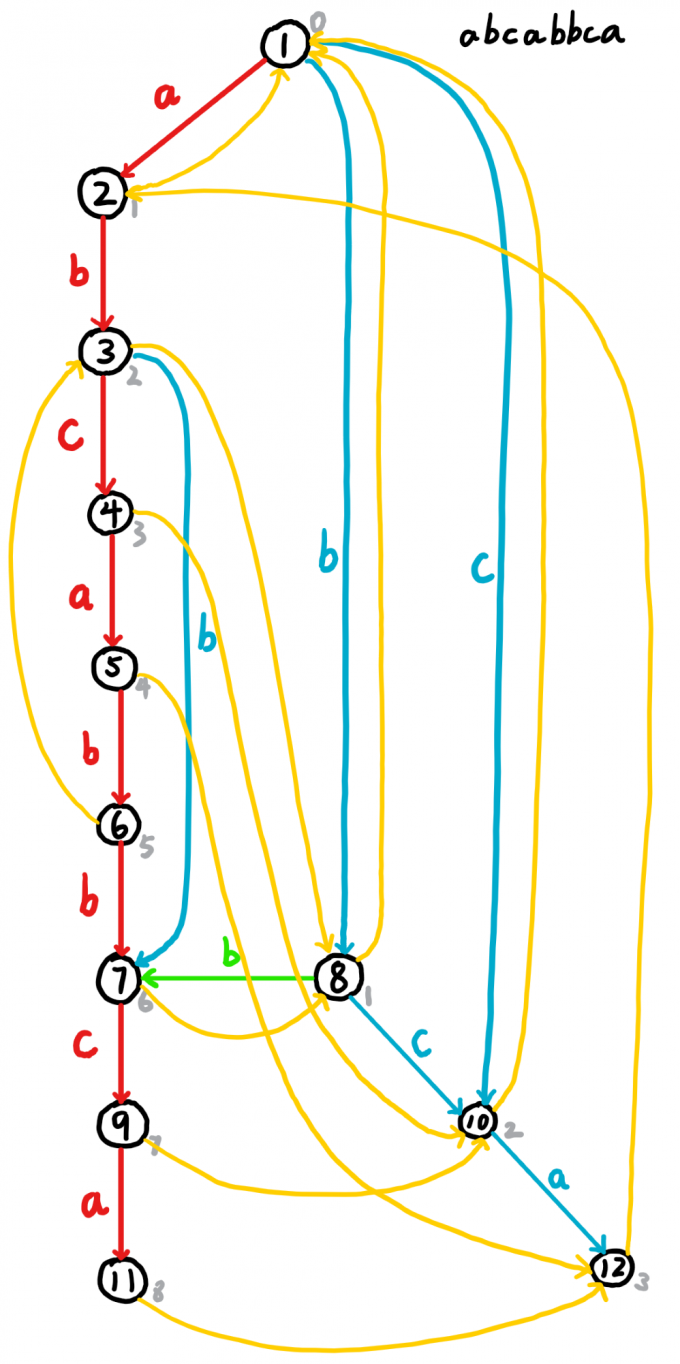
(注意点12到点6少了一条边b)
$\ \ \ \ \ \ \ \,$其中我们如下规定:
红色,蓝色,绿色的边构成一个尾部收束的$Trie$树,用来高效表示这个串的后缀集合,就是$son$数组构成的。并且我们把红色的链叫做主链,蓝色叫做扩展链,同一水平面的点叫做扩展点对(在模板中,每个$last$的取值都是主链,每个$np$和$nq$都是扩展点对)
(都是我自己取的名字)黄色构成$parents$树,就是$fa$数组构成的,这棵树爸爸不认儿子,儿子认爸爸。
在点旁边的灰色数字就是$len$数组。
$\ \ \ \ \ \ \ \,$其实这张图看上去还是挺麻烦的,我们不如将它分开来看:
尾部收束的$Trie$树:
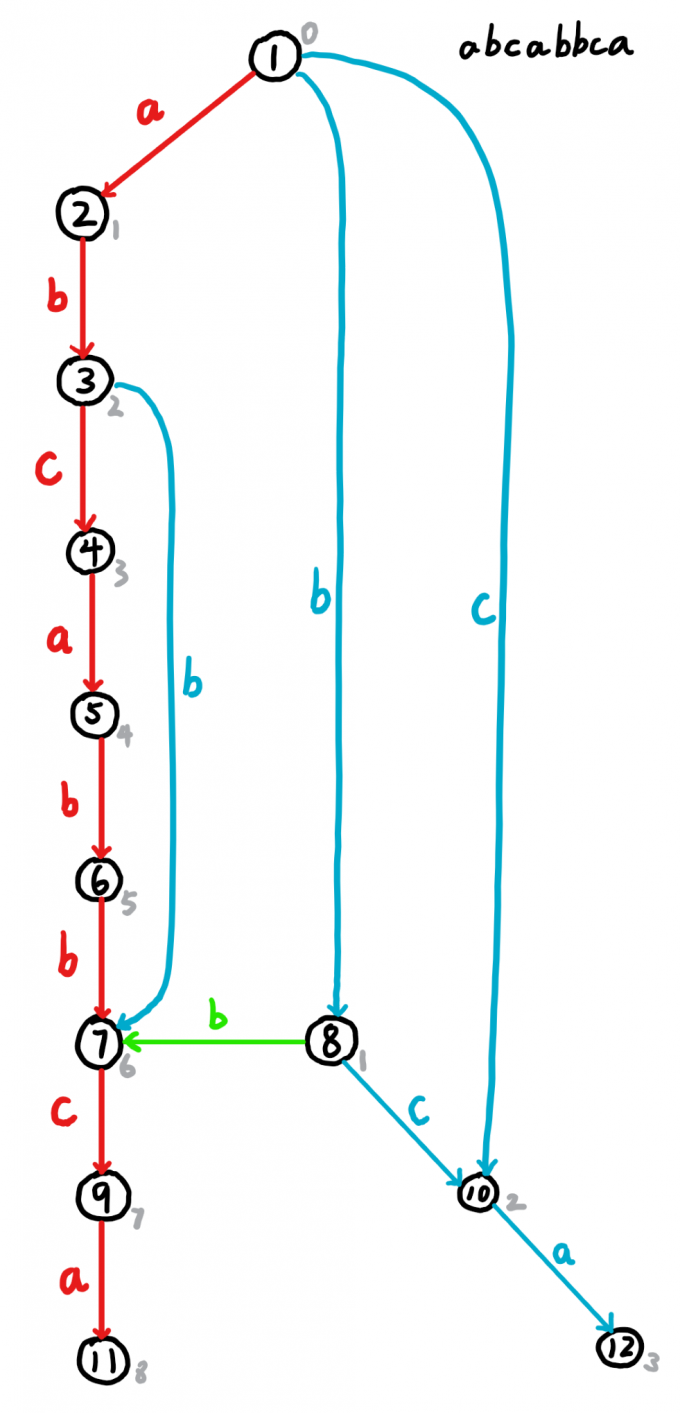
(注意点12到点6少了一条边b)
$\ \ \ \ \ \ \ \,$尾部收束的$Trie$树,用来高效表示这个串的后缀集合,可以发现,我们从节点 $1$ 开始走,在走到没有儿子的节点的时候,必然是原串的一个后缀,并且是覆盖完了的,换句话说,这个串的任意子串都可以在这棵树上表示出来,且仅有这个串的子串才能表示。
$\ \ \ \ \ \ \ \,$不妨来观察一下,每一个节点上都有哪些子串的信息:
2:a
3:ab
4:abc
5:abca
6:abcab,bcab,cab
7:abcabb,bcabb,cabb,abb,bb
8:b
9:abcabbc,bcabbc,cabbc,abbc,bbc
10:bc,c
11:abcabbca,bcabbca,cabbca,abbca,bbca
12:bca,ca
$\ \ \ \ \ \ \ \,$这样一来,很多性质都出来了:
在$Trie$上,父亲是儿子上的子串的公共前缀(废话);
在主链上的点,最长的子串都是原串的前缀;
在一个点上的子串,短的为长的的后缀;
$len$数组表示的是这个节上的子串最长长度;
扩展点对一个在主链上一个在扩展链上,在扩展链上的点上的子串是在主链上的点上的子串的公共后缀。
$parents$树:
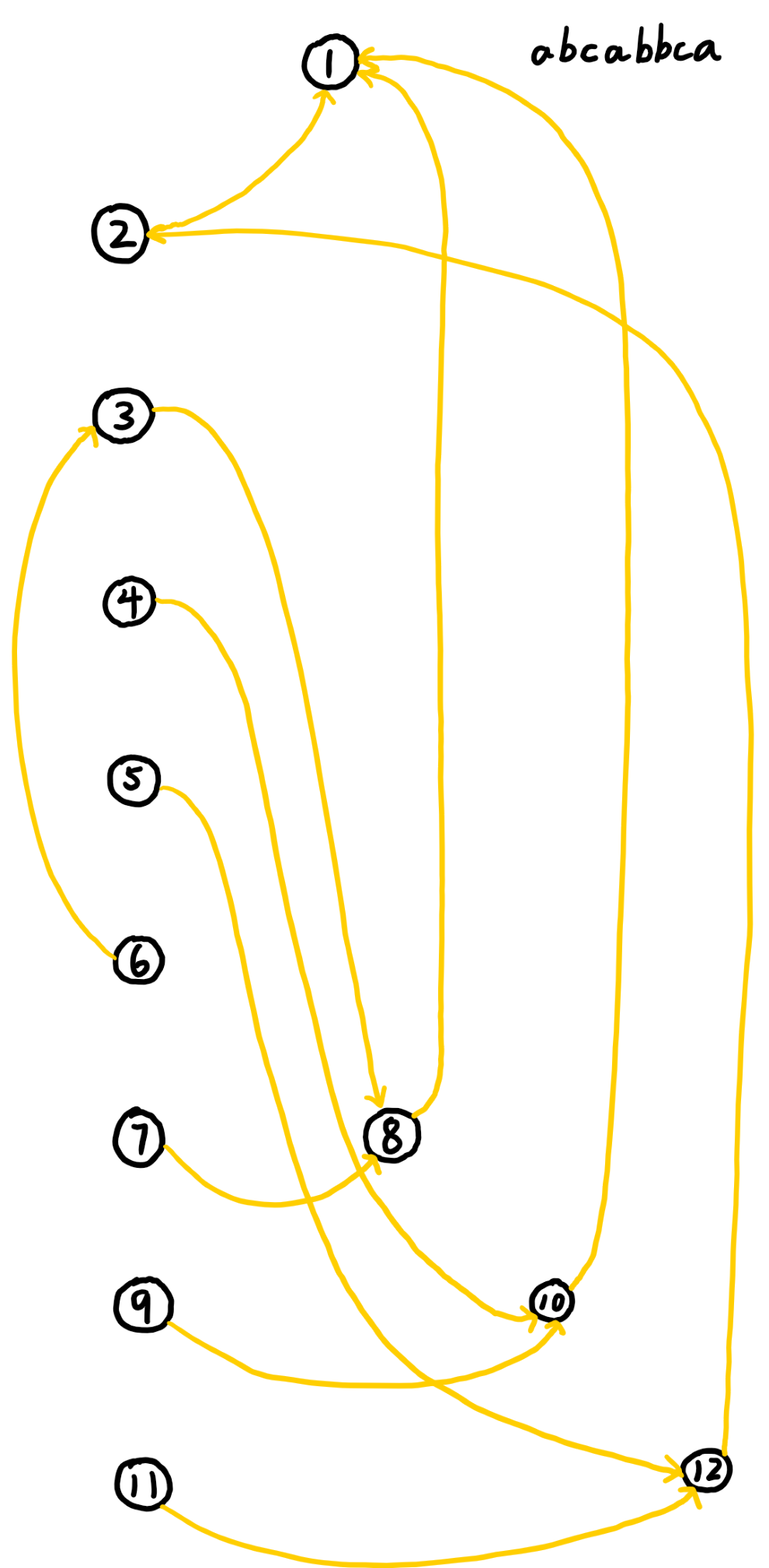
$\ \ \ \ \ \ \ \,$这样看起来好像不是特别方便,我们把他整合一下:
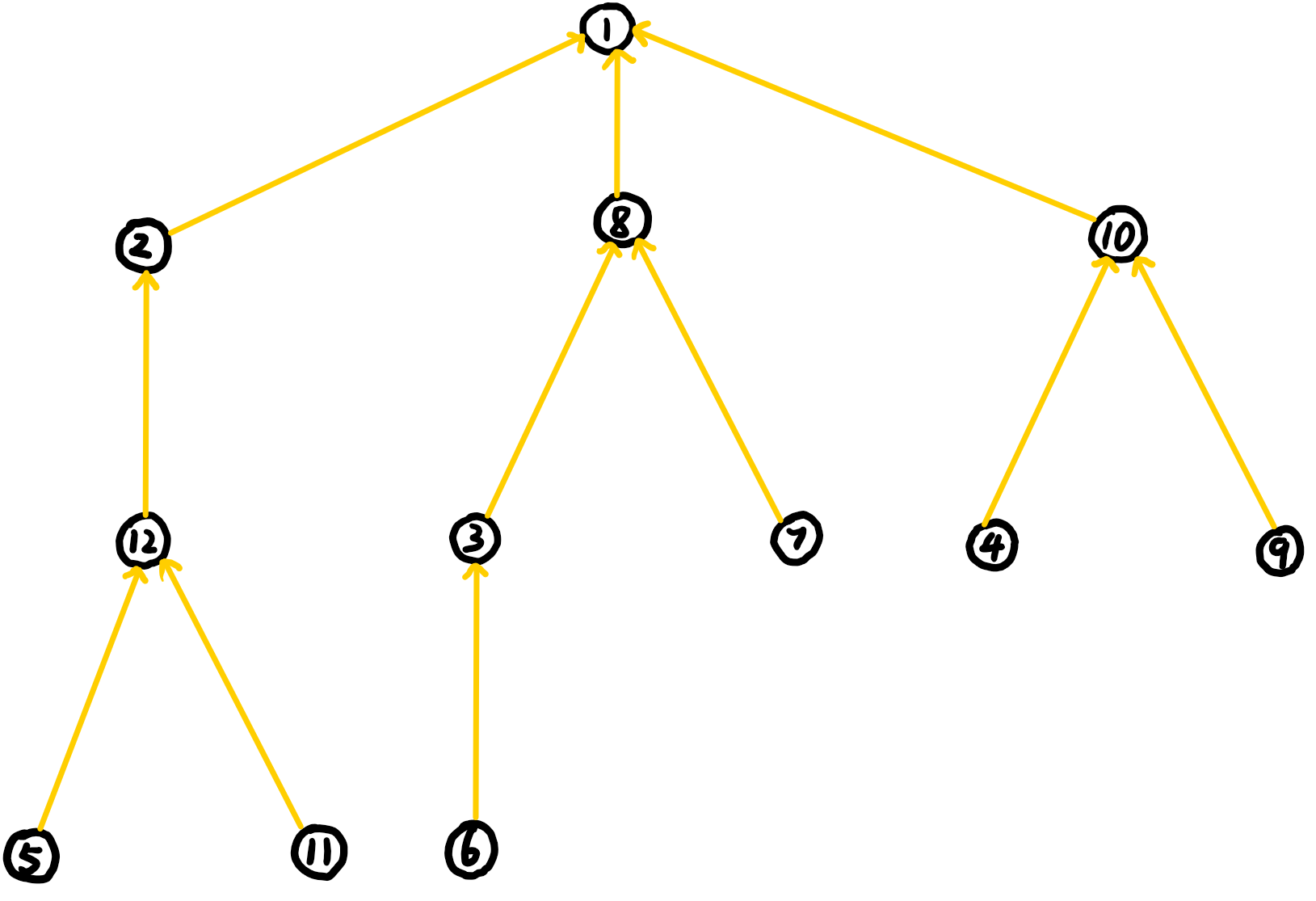
$\ \ \ \ \ \ \ \,$回想一下每一个节点上都有哪些子串的信息和出现次数,顺便看看每个子串出现的终点:
2:a (3:1,4,8)
3:ab (2:2,5)
4:abc (1:3)
5:abca (1:4)
6:abcab (1:5),bcab (1:5),cab (1:5)
7:abcabb (1:6),bcabb (1:6),cabb (1:6),abb (1:6),bb (1:6)
8:b (3:2,5,6)
9:abcabbc (1:7),bcabbc (1:7),cabbc (1:7),abbc (1:7),bbc (1:7)
10:bc (2:3,7),c (2:3,7)
11:abcabbca (1:8),bcabbca (1:8),cabbca (1:8),abbca (1:8),bbca (1:8)
12:bca (2:4,8),ca (2:4,8)
$\ \ \ \ \ \ \ \,$很多性质又都出来了:
在$parents$上,父亲是儿子上的子串的公共后缀;
叶子节点都是主链上的节点;
主链上的节点上的子串的出现终点,都有$len$数组描述的位置;
一个节点上的子串出现次数是一样的;
父亲上的子串出现次数,是儿子上的子串出现次数之和;
儿子上的子串出现的终点,是父亲上的子串出现的终点的子集;
点$i$上面表示子串的数量为$len[fa[i]]-len[i]$。
$\ \ \ \ \ \ \ \,$最后我们总结一下:
在$Trie$上,父亲是儿子上的子串的公共前缀;
在$parents$上,父亲是儿子上的子串的公共后缀;
在一个点上的子串,短的为长的的后缀;
一个节点上的子串出现次数是一样的;
$len$数组表示的是这个节上的子串最长长度;
$parents$上叶子节点都是主链上的节点;
在主链上的点,最长的子串都是原串的前缀;
主链上的节点上的子串的出现终点,都有$len$数组描述的位置;
扩展点对一个在主链上一个在扩展链上,在扩展链上的点上的子串是在主链上的点上的子串的公共后缀;
$parents$上父亲上的子串出现次数,是儿子上的子串出现次数之和,如果父亲在主链上,就再加一;
$parents$上儿子上的子串出现的终点,是父亲上的子串出现的终点的子集;
点$i$上面表示子串的数量为$len[fa[i]]-len[i]$。
$\ \ \ \ \ \ \ \,$如此多的性质,我们就可以拿后缀自动机解决很多问题了:
字符串匹配
文本串建立后缀自动机,模式串在$Trie$上面跑一次,跑完了就匹配到了,利用了$Trie$上面包含了原串所有子串的性质,多文本串的话,就在文本串之间插入奇怪字符,然后一起建立后缀自动机就行了就可以解决了,或者建广义后缀自动机。
子串查询出现次数
文本串建立后缀自动机,然后在$parents$上做$dp$,询问就让模式串在$Trie$上面跑一次,找到自动机上点,输出就好了,利用了$parents$上父亲上的子串出现次数,是儿子上的子串出现次数之和的性质。因为$parents$上是儿子认爸爸,爸爸不认儿子,所以我们需要跑个拓扑,拓扑序就是$y$的倒叙了啊:
1 | for(int i=1;i<=size;i++)x[len[i]]++; |
子串查询出现位置
文本串建立后缀自动机,让模式串在$Trie$上面跑一次,找到自动机上点,再从这个点开始,在$parents$上跑,遇到在主链上的点,它的$len$值就是终点了,要是求起点坐标,终点减去长度加上$1$就好了。
最长回文串
文本串倍增,后半截翻转,查询子串出现次数大于$2$,并且位置换算一下,如果相解就是合法,取最大值就好了,实现起来略复杂,没有Manacher算法优秀。
子串的子串
子串的子串要么是它的前缀的后缀,要么是它的前缀,要么是他的后缀,所以说只需要找到子串这个点,他在$parents$上的子树和他在$Trie$的祖先,还有他在$parents$上的子树的$Trie$的祖先,都是他的子串。
后缀自动机的合并(广义后缀自动机)
后缀自动机的合并,我们可以理解为,在后缀自动机上新加入一个字符串,其实只需要将 $last$ 重新赋为 $1$ ,注意新串的点打上不一样的标记,这个差不多就是广义后缀自动机,广义后缀自动机还有一步判断这个点有没有被建过的操作,但个人感觉实际上没有必要,最坏空间复杂度依然是$O(2nm)$的:
1 | void Insert(char *s){ |
$\ \ \ \ \ \ \ \,$还有很多关于子串,前缀,后缀的问题或者可以转换为子串,前缀,后缀的问题,用后缀自动机在大多数情况下都是不二之选,一般字符串的字符集都比较小,所以复杂度也很优秀,但要是字符集大小太大的话,还是仔细想想其他算法吧。
$\ \ \ \ \ \ \ \,$还有,后缀自动机处理的字符串是静态的,最多就是在后面加后缀,要是需要处理动态的字符串的话,多半也是不合算的,需要考虑其他算法。
$\ \ \ \ \ \ \ \,$不过,后缀自动机依然是一个优秀的字符串数据结构,代码量小,适用性高,是一个万金油算法。