$\ \ \ \ \ \ \ \,$图论基础复习笔记:
存图相关
1.邻接表:
$\ \ \ \ \ \ \ \,$在点数特别小的时候,我们可以用邻接表(二维数组)来表示点之间的链接关系。
1
2
| int e[N][N];
void add(int a,int b,int w){e[a][b]=w;}
|
2. 链表:
$\ \ \ \ \ \ \ \,$在点数比较大的时候,我们可以用链式向前星来表示点之间的链接关系。
1
2
3
4
| int head[N],p;
struct Edge{int v,w,last;}E[N];
void add(int a,int b,int w)
{E[++p]=(Edge){b,w,head[a]};head[a]=p;}
|
$\ \ \ \ \ \ \ \,$遍历方式如下:
1
2
| for(int i=head[u];i;i=G[i].last)G[i].v,G[i].w;
|
3.动态数组
$\ \ \ \ \ \ \ \,$在点数比较大的时候,我们可以用$\tt vector$,会比链表慢一点,但是比较方便,下面默认都是这种存图方法。
1
2
3
4
| struct Edge{int p,w;}E[N];
vector<Edge> e[N];
void add(int a,int b,int w)
{e[a].push_back((Edge){b,w});}
|
$\ \ \ \ \ \ \,$遍历方式如下:
1
2
| for(auto v:E[u])v.p,v.w;
|
最短路
$\ \ \ \ \ \ \ \,$最短路的核心思想都差不多,用松弛操作来求解,所以只讲算法特点和用法,不讲原理:
1.Floyd
$\ \ \ \ \ \ \ \,$Floyd可以在$O(n^3)$的时间内,求出任意点对两两之间的距离,支持负边权:
1
2
3
4
5
6
7
8
9
10
11
12
13
| int dis[N][N];
void floyd(){
memset(dis,63,sizeof(dis));
for(int i=1;i<=n;i++){
dis[i][i]=0;
for(auto v:E[i])dis[i][v.p]=v.w;
}
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(dist[i][j]>dist[i][k]+dist[k][j])
dist[i][j]=dist[i][k]+dist[k][j];
}
|
2.SPFA
$\ \ \ \ \ \ \ \,$SPFA可以在下到$n$上到$(n^2)$的时间内,求出单源对于每个点最短路,支持负边权,但是因为复杂度不平衡,关于SPFA,他死了:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| int dis[N];
bool used[N];
queue<int> Q;
void SPFA(int S){
memset(dis,63,sizeof(dis));
Q.push(S);used[S]=1;dis[S]=0;
while(!Q.empty()){
int u=Q.front();Q.pop();used[u]=0;
for(auto v:E[u])
if(dis[v.p]>dis[u]+v.w){
dis[v.p]=dis[u]+v.w;
if(used[v.p]==0)
{used[v.p]=1;Q.push(v.p);}
}
}
}
|
$\ \ \ \ \ \ \ \,$或者SPFA加上堆优化后,复杂度会比较好,长得也和Dijkstra很相像了:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| struct node{int v,dis;};
inline bool operator <(const node &a,const node &b)
{return a.dis>b.dis;}
int dis[N];
priority_queue<node> Q;
void heap_SPFA(int S){
memset(dis,63,sizeof(dis));
Q.push((node){1,0});
dis[S]=0;used[S]=1;
while(!Q.empty()){
int u=Q.top().v;Q.pop();used[u]=0;
for(auto v:E[u])
if(dis[v.p]>dis[u]+v.w){
dis[v.p]=dis[u]+v.w;
if(used[v.p]==0)
{used[v.p]=1;Q.push((node){dis[v.p],v.p})};
}
}
}
|
3.Dijkstra
$\ \ \ \ \ \ \ \,$Dijkstra可以在$O(n\log n)$的时间内,求出单源对于每个点最短路,但是不支持负边权:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| struct node{int v,dis;};
inline bool operator <(const node &a,const node &b)
{return a.dis>b.dis;}
int dis[N];
priority_queue<node> Q;
void Dijkstra(int S){
memset(dis,63,sizeof(dis));
Q.push((node){1,0});dis[S]=0;
while(!Q.empty()){
int u=Q.top().v;Q.pop();
for(auto v:E[u])
if(dis[v.p]>dis[u]+v.w){
dis[v.p]=dis[u]+v.w;
Q.push((node){dis[v.p],v.p});
}
}
}
|
生成树
$\ \ \ \ \ \ \ \,$生成树是针对无向图的说法,基本上是基于贪心的操作。
1.最小生成树
$\ \ \ \ \ \ \ \,$最小生成树最常见的贪心做法是Kruskal,因为一棵树$n-1$条边,我们可以把所有边排序过后,贪心选取能构成树的最小的$n-1$条边,用并查集维护其连通性:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| int top,fa[N];
struct Link{int u,v,w;}e[N];
inline bool operator <(const Link &a,const Link &b){return a.w<b.w;}
int find(int a){return a==fa[a]?a:fa[a]=find(fa[a]);}
void add_edge(int a,int b,int w){e[++top]=(Link){a,b,w};}
void Kruskal(){
sort(e+1,e+top+1);
for(int i=1;i<=n;i++)fa[i]=i;
for(int i=1,A,B;i<=m;i++)
if((A=find(e[i].u))!=(B=find(e[i].v))){
add(e[i].u,e[i].v,e[i].w);
add(e[i].v,e[i].u,e[i].w);
fa[A]=B;
}
}
|
2.次小生成树\k小生成树\严格次小生成树
$\ \ \ \ \ \ \ \,$次小生成树,我们就是做如下操作:
做一次最小生成树;
在没有加入树边的边中选一个最小的,假设为u与v之间的边;
在最小生成树上面$u$到$v$的路径上,删除一条最长的边;
然后把2步中选择的边加入树边。
$\ \ \ \ \ \ \ \,$复杂度是$O(m\log m+n\log n)$,操作比较繁琐,虽然有些时候不需要真实建树,但是还是很繁琐,就不单独贴模板了。
$\ \ \ \ \ \ \ \,$对于k小生成树,我们做k次就好了啊,复杂度$O(m\log m+kn\log n)$。
$\ \ \ \ \ \ \ \,$对于严格次小生成树,我们做最多$m$次,检查直到严格大于最小生成树就停止,复杂度$O(m\log m+mn\log n)$。
$\ \ \ \ \ \ \ \,$代码很长,引起不适:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
| #include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<cctype>
#include<cstdio>
#include<vector>
#include<string>
#include<queue>
#include<stack>
#include<cmath>
#include<map>
#include<set>
using namespace std;
const long long inf=2147483647000000;
const double eps=1e-10;
const double pi=acos(-1.0);
inline int read(){
int x=0,f=1;char ch;ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-') f=0;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch&15);ch=getchar();}
if(f)return x;else return x;
}
const int N=900010;
int n,m;
long long Cnt;
bool used[N];
struct Edge{int p,w;}E[N];
vector<Edge> G[N<<1];
void add(int a,int b,int w)
{G[a].push_back((Edge){b,w});}
int top,Fa[N];
struct Link{int u,v,w;}e[N];
inline bool operator <(const Link &a,const Link &b){return a.w<b.w;}
int find(int a){return a==Fa[a]?a:Fa[a]=find(Fa[a]);}
void add_edge(int a,int b,int w){e[++top]=(Link){a,b,w};}
void Kruskal(){
sort(e+1,e+top+1);
for(int i=1;i<=n;i++)Fa[i]=i;
for(int i=1,A,B;i<=m;i++)
if((A=find(e[i].u))!=(B=find(e[i].v))){
add(e[i].u,e[i].v,e[i].w);
add(e[i].v,e[i].u,e[i].w);
Cnt+=1ll*e[i].w;
used[i]=1;
Fa[A]=B;
}
}
int fa[N][19],deep[N];
long long Max[N][19],Min[N][19];
void dfs(int u,int f){
fa[u][0]=f;
for(auto v:G[u]){
if(v.p==f)continue;
deep[v.p]=deep[u]+1;
Max[v.p][0]=v.w;
Min[v.p][0]=-inf;
dfs(v.p,u);
}
}
void cal(){
for(int i=1;i<=18;++i)
for(int j=1;j<=n;++j){
fa[j][i]=fa[fa[j][i-1]][i-1];
Max[j][i]=max(Max[j][i-1],Max[fa[j][i-1]][i-1]);
Min[j][i]=max(Min[j][i-1],Min[fa[j][i-1]][i-1]);
if(Max[j][i-1]>Max[fa[j][i-1]][i-1])
Min[j][i]=max(Min[j][i],Max[fa[j][i-1]][i-1]);
else if(Max[j][i-1]<Max[fa[j][i-1]][i-1])
Min[j][i]=max(Min[j][i],Max[j][i-1]);
}
}
int LCA(int x,int y){
if(deep[x]<deep[y])swap(x,y);
for(int i=18;i>=0;--i)
if(deep[fa[x][i]]>=deep[y])x=fa[x][i];
if(x==y)return x;
for(int i=18;i>=0;--i)
if(fa[x][i]!=fa[y][i])x=fa[x][i],y=fa[y][i];
return fa[x][0];
}
long long qmax(int u,int v,long long maxx){
long long Ans=-inf;
for(int i=18;i>=0;--i)
if(deep[fa[u][i]]>=deep[v]){
if(maxx!=Max[u][i])Ans=max(Ans,Max[u][i]);
else Ans=max(Ans,Min[u][i]);
u=fa[u][i];
}
return Ans;
}
int main()
{
n=read(),m=read();
for(int i=1,a,b,c;i<=m;i++)
a=read(),b=read(),c=read(),
add_edge(a,b,c);
Kruskal();
long long Ans=inf;
Min[1][0]=-inf;
deep[1]=1;
dfs(1,-1);cal();
for(int i=1;i<=m;++i)if(!used[i]){
int u=e[i].u,v=e[i].v,lca=LCA(u,v);
long long d=e[i].w;
Ans=min(Ans,Cnt-max(qmax(u,lca,d),qmax(v,lca,d))+d);
}
printf("%lld",Ans);
return 0;
}
|
3.斯坦纳树
$\ \ \ \ \ \ \ \,$当只要求图的一部分点连接的时候,求最小的生成树,就是斯坦纳树,做法比较繁琐,大数据也不能优秀地处理。具体看这里【斯坦纳树学习笔记(VictoryCzt Orz)】。
生成树形图
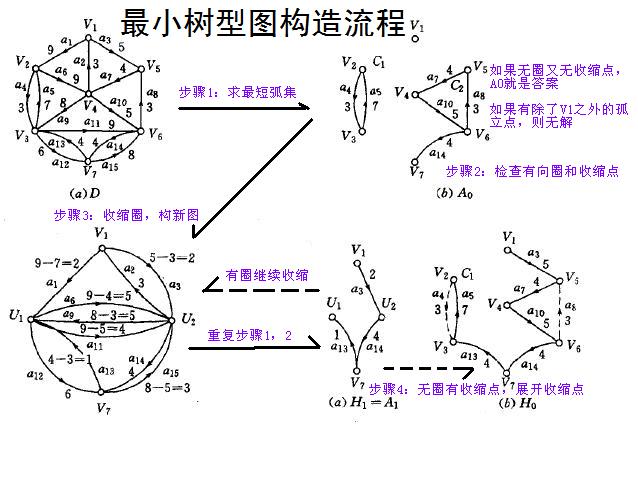
$\ \ \ \ \ \ \ \,$树形图不是一个有很好求法的东西,朱刘算法可以做到复杂度$O(nm)$求出最小树形图,过程大概如下:
找到除了$root$以为其他点的权值最小的入边,如果出现除了$root$以外存在其他孤立的点,则不存在最小树形图。
找到图中所有的环,并对环进行缩点,重新编号,更新其他点到环上的点的距离。
以环数为下一次查找的点数,继续执行上述操作,直到没有环或者判定出不存在最小树形图为止。
$\ \ \ \ \ \ \ \,$大概就是这个图的意思:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| int n,root;
int k[N],idx[N],x,tim;
int cost[N],fa[N],f[N];
int mincost[N],ans,top;
struct Link{int u,v,w;}e[N];
inline bool operator <(const Link &a,const Link &b){return a.w<b.w;}
void add_edge(int a,int b,int w){e[++top]=(Link){a,b,w};}
int Zhu_Liu(int root){
while(1){
memset(mincost,63,sizeof(mincost));
memset(idx,-1,sizeof(idx));
memset(f,0,sizeof(f));
for(int i=1;i<=m;i++)
if(e[i].w<mincost[e[i].v]&&e[i].u!=e[i].v)
{mincost[e[i].v]=e[i].w;fa[e[i].v]=e[i].u;}
mincost[root]=0;tim=0;
for(int i=1;i<=n;i++){
if(mincost[i]==mincost[0])return 1;
ans+=mincost[i];x=i;
while(f[x]!=i&&x!=root)f[x]=i,x=fa[x];
if(x!=root&&idx[x]==-1){
tim++;
for(int j=fa[x];j!=x;j=fa[j])idx[j]=tim;
idx[x]=tim;
}
}
if(tim==0)break;
for(int i=1;i<=n;i++)
if(idx[i]==-1)idx[i]=++tim;
for(int i=1;i<=m;i++){
x=e[i].v;e[i].u=idx[e[i].u];e[i].v=idx[e[i].v];
if(e[i].u!=e[i].v)e[i].w-=mincost[x];
}
n=tim;root=idx[root];
}
return ans;
}
|
生成树和生成树形图计数
$\ \ \ \ \ \ \ \,$计数的话,需要用到矩阵树定理:
$\ \ \ \ \ \ \ \,$图基尔霍夫矩阵的行列式值就是图的生成树个数
$\ \ \ \ \ \ \ \,$对于生成树形图同样适用,把双向边和入度改为单向即可,通过线性代数技巧优化求行列式的复杂度,可以做到$O(n^3+nm)$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| int A[N][N];
void add(int a,int b){
A[a][a]++;A[b][b]++;
A[a][b]--;A[b][a]--;
}
int Gauss(){
int ans=1;
for(int i=1;i<n;i++){
for(int j=i+1;j<n;j++)
while(A[j][i]){
int t=A[i][i]/A[j][i];
for(int k=i;k<n;k++)
A[i][k]-=t*A[j][k];
swap(A[j],A[i]);
ans=-ans;
}
ans*=A[i][i];
}
return ans
}
|
